You may have heard the term depth of field (DoF), but if you are new to photography you may not yet be taking advantage of how DoF can enhance your photos.
A basic definition of depth of field is: the zone of acceptable sharpness within a photo that will appear in focus. In every picture there is a certain area of your image in front of, and behind the subject that will appear in focus.
This zone will vary from photo to photo. Some images may have very small zones of focus which is called shallow depth of field.
Three main factors that will affect how you control the depth of field of your images are: aperture (f-stop), distance from the subject to the camera, and focal length of the lens on your camera. Here are some explanations and answers to other common questions concerning depth of field.
How does aperture control depth of field?
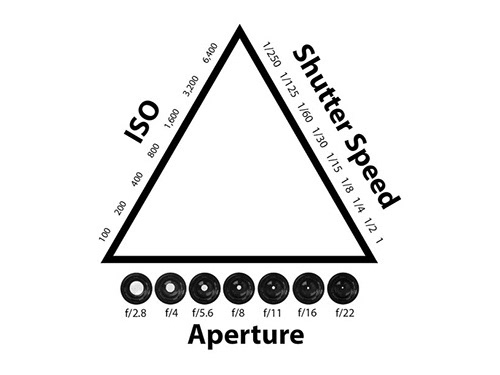
Aperture refers to the access given to light from the lens to the camera sensors. The size of your aperture (the diameter of the hole through which light enters the camera) controls the amount of light entering your lens. Using the aperture (f-stop) of your lens is the simplest way to control your depth of field as you set up your shot.
Large aperture = Small f-number = Shallow (small) depth of field
Small aperture = Larger f-number = Deeper (larger) depth of field
Small aperture = Larger f-number = Deeper (larger) depth of field
It may be easier to remember this simple concept: The lower your f-number, the smaller your depth of field. Likewise, the higher your f-number, the larger your depth of field. For example, using a setting of f/2.8 will produce a very shallow depth of field while f/11 will produce a deeper DoF.
How does distance control depth of field?
The closer your subject is to the camera, the shallower your depth of field becomes. Therefore, moving further away from your subject will deepen your depth of field.
How does the focal length of a lens control depth of field?
Focal Length refers to the capability of a lens to magnify the image of a distant subject. This can get complicated, but the simple answer is that the longer you set your focal length the shallower the depth of field. Example: Your subject is 10 meters (33 feet) away, using a focal length of 50mm at f/4; your depth of field range would be from 7.5 -14.7 meters (24.6-48 feet) for a total DOF of 7.2 meters (23.6 feet). If you zoom into 100mm from the same spot, the depth of field changes to 9.2-10.9m (30.1-35.8′) for a total of 1.7m (5.7′) of depth of field. But if you move to 20m (66′) away from your subject using the 100mm lens, your depth of field is almost the same as it would be at 10 meters using a 50mm lens.
The Field of View, F.O.V for short, includes everything seen through the viewfinder for a given focal length.
Larger focal lengths, producing smaller fields of view, zoom in or magnify the subject, isolating it in the composition, such as a close-up of an animal in nature.
Smaller focal lengths, producing larger fields of view, zoom out, showing more of a scene. For example, a broad & distant landscape.
Focal length also has an effect on depth of field, as taught below.
The photographer can adjust the focal length to select the desired field of view. Doing so determines outside boundaries of the image composition.
The focal length range provides the maximum and minimum focal lengths the photographer can select for a given lens.
Wide Angle, Standard, & Telephoto Lenses
Human vision is approximately 50mm focal length. Compared to standard vision, focal lengths larger than 50mm will magnify a scene, producing a smaller field of view.
Focal lengths smaller than 50mm will produce a “wide angle view”. This creates a field of view wider than normal human vision.
Objects in this field of view tend to become smaller and slightly distorted, compared to what we are used to seeing.
Wide Angle Lenses produce a field of view larger than our standard vision & usually range from 8mm to 35mm in focal length.
Standard Lenses produce a field of view similar to our standard vision & usually range from 40mm to 60mm in focal length.
Telephoto Lenses produce a field of view smaller than our standard vision & usually exceed 70mm in focal length.
Object field calculation methods
Traditional depth-of-field formulas can be hard to use in practice. As an alternative, the same effective calculation can be done without regard to the focal length and f-number.Moritz von Rohr and later Merklinger observe that the effective absolute aperture diameter can be used for similar formula in certain circumstances.
Moreover, traditional depth-of-field formulas assume equal acceptable circles of confusion for near and far objects. Merklinger suggested that distant objects often need to be much sharper to be clearly recognizable, whereas closer objects, being larger on the film, do not need to be so sharp. The loss of detail in distant objects may be particularly noticeable with extreme enlargements. Achieving this additional sharpness in distant objects usually requires focusing beyond the hyperfocal distance, sometimes almost at infinity. For example, if photographing a cityscape with a traffic bollard in the foreground, this approach, termed the object field method by Merklinger, would recommend focusing very close to infinity, and stopping down to make the bollard sharp enough. With this approach, foreground objects cannot always be made perfectly sharp, but the loss of sharpness in near objects may be acceptable if recognizability of distant objects is paramount.
Other authors such as Ansel Adams have taken the opposite position, maintaining that slight unsharpness in foreground objects is usually more disturbing than slight unsharpness in distant parts of a scene.
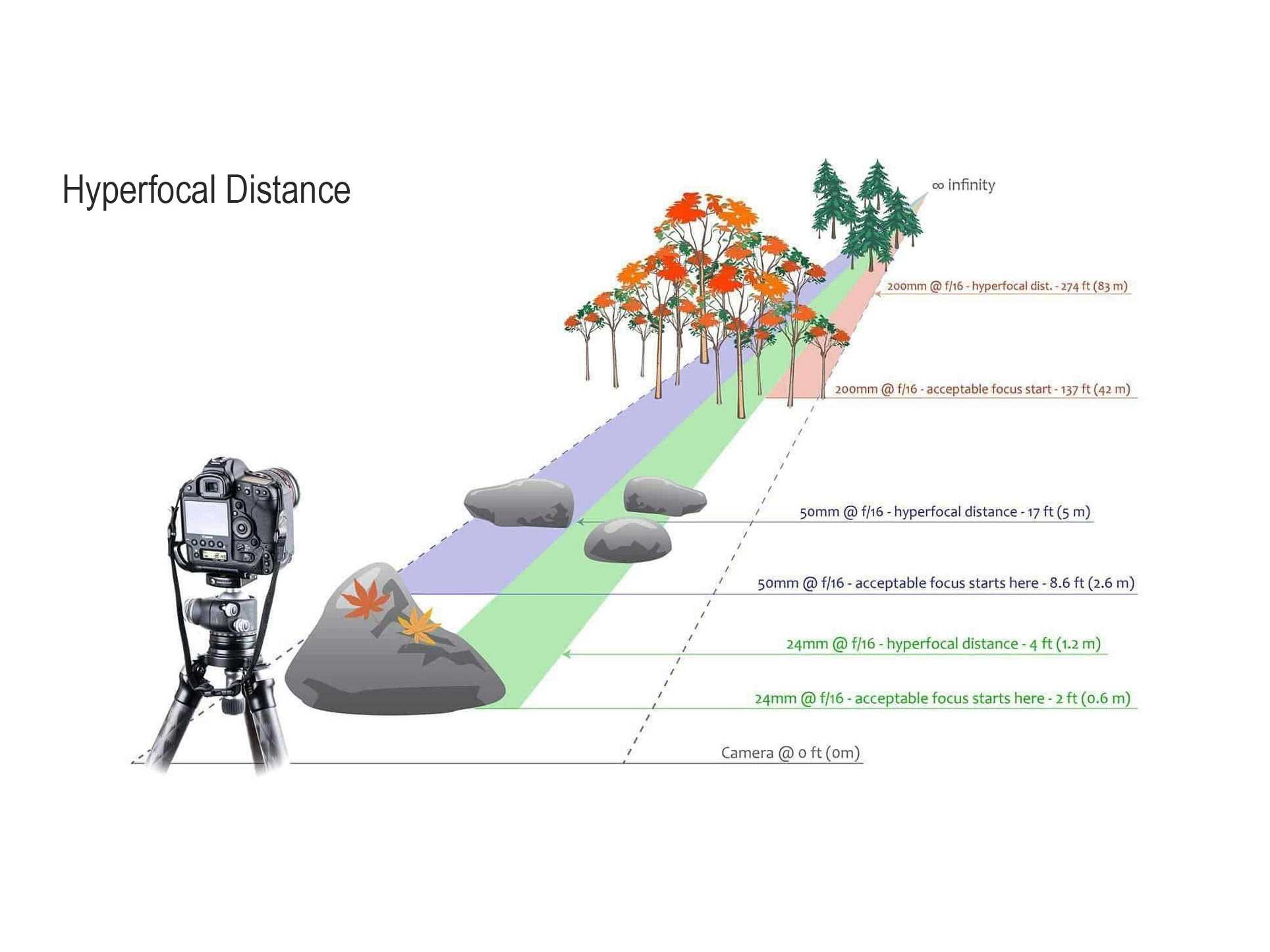
Hyperfocal distance
In optics and photography, hyperfocal distance is a distance beyond which all objects can be brought into an "acceptable" focus. As the hyperfocal distance is the focus distance giving the maximum depth of field, it is the most desirable distance to set the focus of a fixed-focus camera.The hyperfocal distance is entirely dependent upon what level of sharpness is considered to be acceptable.
The hyperfocal distance has a property called "consecutive depths of field", where a lens focused at an object whose distance is at the hyperfocal distance H will hold a depth of field from H/2 to infinity, if the lens is focused to H/2, the depth of field will extend from H/3 to H; if the lens is then focused to H/3, the depth of field will extend from H/4 to H/2, etc.
Thomas Sutton and George Dawson first wrote about hyperfocal distance (or "focal range") in 1867. Louis Derr in 1906 may have been the first to derive a formula for hyperfocal distance. Rudolf Kingslake wrote in 1951 about the two methods of measuring hyperfocal distance.
Zeiss Ikon Contessa with red marks for hyperfocal distance 20 ft at f/8
Some cameras have their hyperfocal distance marked on the focus dial. For example, on the Minox LX focusing dial there is a red dot between 2 m and infinity; when the lens is set at the red dot, that is, focused at the hyperfocal distance, the depth of field stretches from 2 m to infinity.